こんにちは。プロ家庭教師集団「名門指導会」算数科主任の高野健一です。入試に向けて算数で特に押さえておきたいポイントについてお話しする3回シリーズ、前回は図形問題を解くポイントを紹介しました。2回目の今回のテーマは「速さ」です。
中学入試の算数において、「速さ」は出題頻度の高い分野の1つです。その一方で、速さを苦手とする子は少なくありません。その大きな理由は、速さの問題では解法を単にあてはめるだけで解決できる問題が少なく、その前に動きの状況を整理することで初めて解決の糸口を見つけることができる問題が多いからです。
速さの問題で動きの状況を整理する方法は、主に次の2つです。
・ダイヤグラム(進行グラフ)
これまでの指導の経験上、多くの子はこれらのうちいずれか一方のみを用いて問題を解こうとするケースが多いです。どちらか一方を使いこなすことができれば、ほとんどの問題は解決できるはずなのですが、実際には一方だけでは行きづまってしまうこともあります。これら2つの方法にはそれぞれ使いやすい場面があるので、それに応じて使い分けができると有利になります。
そこで今回は、「状況図」「ダイヤグラム」がそれぞれ有効に作用する問題を1問ずつ扱い、これらの描き方や有効な活用法について見ていきます。
時間の要素が少なければ状況図を作る
速さの問題を整理する際に、次のような図にまとめることがよくあります。
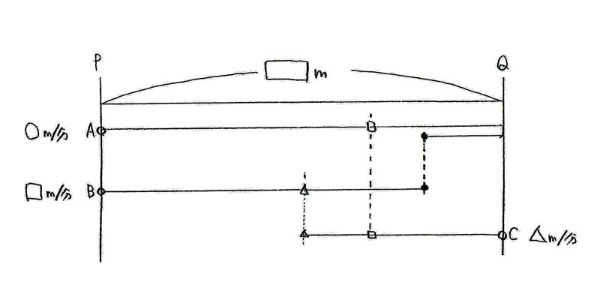
この図は「状況図」や「線分図」などと呼ばれています。線分図という名称は和差算や相当算などでも用いられるので、子どもたちにはなじみがあると思います。しかし、そちらでは数量の大きさを線の長さで表しているのに対し、この場合は動いた様子を線で表しているので、その違いを明確にするために、この記事では「状況図」と呼ぶことにします。
状況図の利点は動いた様子が視覚的に分かりやすいことです。そのため、
動いた距離の和や差に注目→旅人算
距離や時間が等しい部分に注目→比の活用
といった場面で見やすくなります。実際に次の問題で考えてみましょう。
(1) 花子さんの家は駅から何mのところにありますか。
(2) 次郎君は学校まであと何mのところにいますか。